As the topic suggests, we are going to see about Practical Byzantine Fault Tolerance(pBFT). In this guide we will cover below points:
Listen to the full article on audio
- what is pBFT?
- Advantages of pBFT
- Limitations of pBFT
What is pBFT?
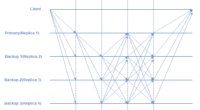
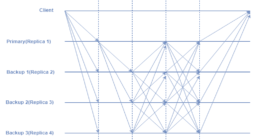
Let’s see the introduction part first. During the late 90s, Barbara Liskov and Miguel Castro introduced Practical Byzantine Fault Tolerance which is a consensus algorithm. Its aim was to answer many queries linked with already existing Byzantine Fault Tolerance solutions. pBFT was designed in such a way that it was capable of working efficiently in asynchronous(no upper bound on when the response to the request will be received) systems. It is utilized for low overhead time. Its application areas involve distributed computing and blockchain.
Its Advantages include below points
- Efficient Energy: Even without carrying out complex mathematical computations pBFT can still achieve distributed consensus. Zilliqa employs pBFT in combination with PoW-like complex computations round for every 100th block.
- Transaction finality: Multiple confirmations are not required to carry out transactions after they have been settled and acknowledged.
- Low reward variance: Each node can be incentivized leading to low variance in rewarding the nodes that help in decision making as every node in the network takes part in replying to clients’ requests.
Besides having advantages, pBFT also has some disadvantages. Let’s see them.
Limitations of pBFT
When the number of nodes in the distributed network is small, The pBFT consensus model works efficiently. However, with increasing nodes in the network, the high communication overhead increases exponentially.
- Sybil attacks: The pBFT mechanisms are exposed to Sybil attacks, in which one entity dominates many identities. With the increasing number of nodes in the network, it becomes hard to carry out Sybil attacks.
- Scaling: pBFT communication(with all the other nodes at every step) overhead is the negative point here. As the number of nodes in the network increases in the form O(n^k), where n is the messages and k is the number of nodes, so does the time taken to reply to the request.






-260x140.png)